Understanding Bayesian Networks
Coding different types of bayes nets and learning their structure and parameters.
The Coding
All the code was written in Python without using any of the pre-existing ML libraries such as tensorflow, sklearn, etc. The code can be found on my GitHub. The following are the highlights of the code:
- Implemented the Independent Bayesian networks with the following structure: The Bayesian network has no edges.
- Learnt the parameters of the independent Bayesian network using the maximum likelihood approach.
- Implemented Tree Bayesian networks. Used the Chow-Liu algorithm to learn the structure and parameters of the Bayesian network as described by Meila and Jordan.
- Implemented the Mixtures of Tree Bayesian networks using EM. The model is defined as follows. We have one latent variable having \(k\) values and each mixture component is a Tree Bayesian network. Thus, the distribution over the observed variables, denoted by \(\textbf{X}\) (variables in the data) is given by:
where \(p_i\) is the probability of the i-th mixture component and \(T_i\) is the distribution represented by the i-th Tree Bayesian network.
-
Learnt the structure and parameters of the model using the EM-algorithm (in the M-step each mixture component is learned using the Chow-Liu algorithm).
-
Implemented the Mixtures of Tree Bayesian networks using Random Forests. The model is defined as above. Learnt the structure and parameters of the model using the following Random-Forests style approach. Given two hyper-parameters \((k, r)\), generate \(k\) sets of Bootstrap samples and learn the \(i\)-th Tree Bayesian network using the \(i\)-th set of the Bootstrap samples by randomly setting exactly \(r\) mutual information scores to 0 (as before use the Chow-Liu algorithm with r mutual information scores set to 0 to learn the structure and parameters of the Tree Bayesian network)
The Experiments
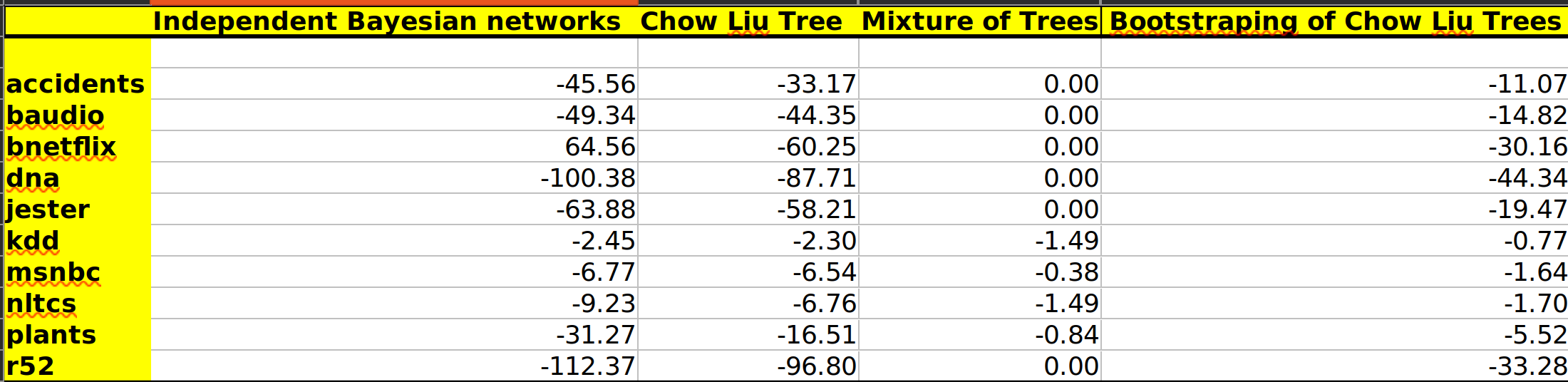
Reported the Test-set Log-Likelihood (LL) score on the 10 datasets as shown in the results below.
The Learnings
I like to categorize my learnings into two categories: The Profound and The Subtle. The Profound are the key questions that were answered through this project. The Subtle could be an intuition I had, insight I discovered or a clever python hack I learnt from this project. For example, print statement has a parameter called end which can be used to change the default newline character to something else.
The Profound
Q1. How well does each approach perform?
Independent Bayesian Networks: This method just assumes that there is no relation between the features and is just solely based on the marginal probabilities of those features. The loglikelihood of the test data for this method is the worst of all the cases for all datasets.
Chow-Liu Tree: This algorithm performs slightly better than the previous one because the tree that is constructed is based on the mutual information matrix which gives a good measure of the dependence of the factors on each other.
Mixture of trees using EM: This method performs the best among all methods for all the datasets. The EM algorithm work very well because of the large number of epochs. The values of K[2, 3, 4] were found out by testing on the validation set for each dataset by checking their loglikelihood on the validation set. The values have been input as a dictionary of key value pairs where keys are the dataset name and the values are the K values. The validation set testing code has been commented out.
Random forest style approach for Mixture of trees: This method gives good likelihood scores too but not as good as the mixture of trees method. The best value for the hyperparameters (K[3, 4], R[5, 6, 7]) were found by testing on the validation set. This algorithm works well because of the bootstrapping.
Note: Another way to set the weight for choosing each mixture model instead of 1/k is weighting them according to the likelihood on the train set. The likelihood values on the train set for each mixture tree was calculated and then normalized to act as weight for the respective tree mixture variables. This gives better performance and makes sense as the mixture tree with more likelihood should have more weight while generating the likelihood of the test set.
The Subtle
- It is tricky working with probabilities. Storing the probs in the table is enlightening as there are very few values stored in each conditional probability table for each feature/random variable.
- Ranking: 1) Mixture of trees using EM 2) Random forest style approach for mixture of trees 3) Chow-Liu trees 4) Independent Bayesian Networks