NeurASP: Embracing Neural Networks into Answer Set Programming
A Neurosymbolic framework that combines Neural networks and Answer Set Programming
Introduction
NeurASP
In this paper there are mainly 2 ideas that the authors explore which are:
- Using pretrained neural network in symbolic computation to improve the neural network’s perception result
- Training a neural network from scratch using ASP rules as constraints.
A neural atom nn() is introduced which represents a neural network in ASP. The idea is to use this atom to invoke a neural network whenever needed inside the ASP program. Some example code to using the neural atom is shown below:
img(d1). img(d2).
nn(digit(1, X), [0,1,2,3,4,5,6,7,8,9]) :- img(X).
addition(A,B,N) :- digit1(A) = N1, digit1(B) = N2, N = N1 + N2.
Learning
The digit1() is an atom that the nn(digit(1, X), [0,1,2,3,4,5,6,7,8,9]) atom is distilled to. In the backend, it is broken down into 10 atoms, one for each digit. The rules above simply state that d1 and d2 are 2 images of digits, digit is the neural network used for the digit classification and the expected output can be any number [0,1,2,3,4,5,6,7,8,9] and the addition of the 2 digits is A. A probability is then associated with each atom digit1(n) where n is a digit, which is simply the output of the neural network. The above program solves the problem of adding 2 digits from images.
Now, to find the sum of two numbers the query in ASP in clingo syntax is given as a constraint :- addition(A,B,1). This query implies that the sum of the 2 digits should be 1. This is what the authors call the observation. Clingo then finds the stable models that satisfy the constraints which are the solution.
The probability of these stable models can be calculated using the following formula: \(\begin{equation}\label{eq_1} P_{\Pi}(I) = \begin{cases} \frac{\prod_{(c = v)} P_{\Pi}(c = v)}{NumStableModels},& \text{if } I \text{ is a stable model of } \Pi \\ 0, & \text{otherwise}\\ \end{cases} \end{equation}\)
in \eqref{eq_1}, $P_{\Pi}(I)$ is the probability of the stable model $I$ given the program $\Pi$. The probability of the observation is simply the sum of probabilities of all the stable models that satisfy the observation. Then the objective becomes to maximize the probability of the observation. Hence gradient ascent!
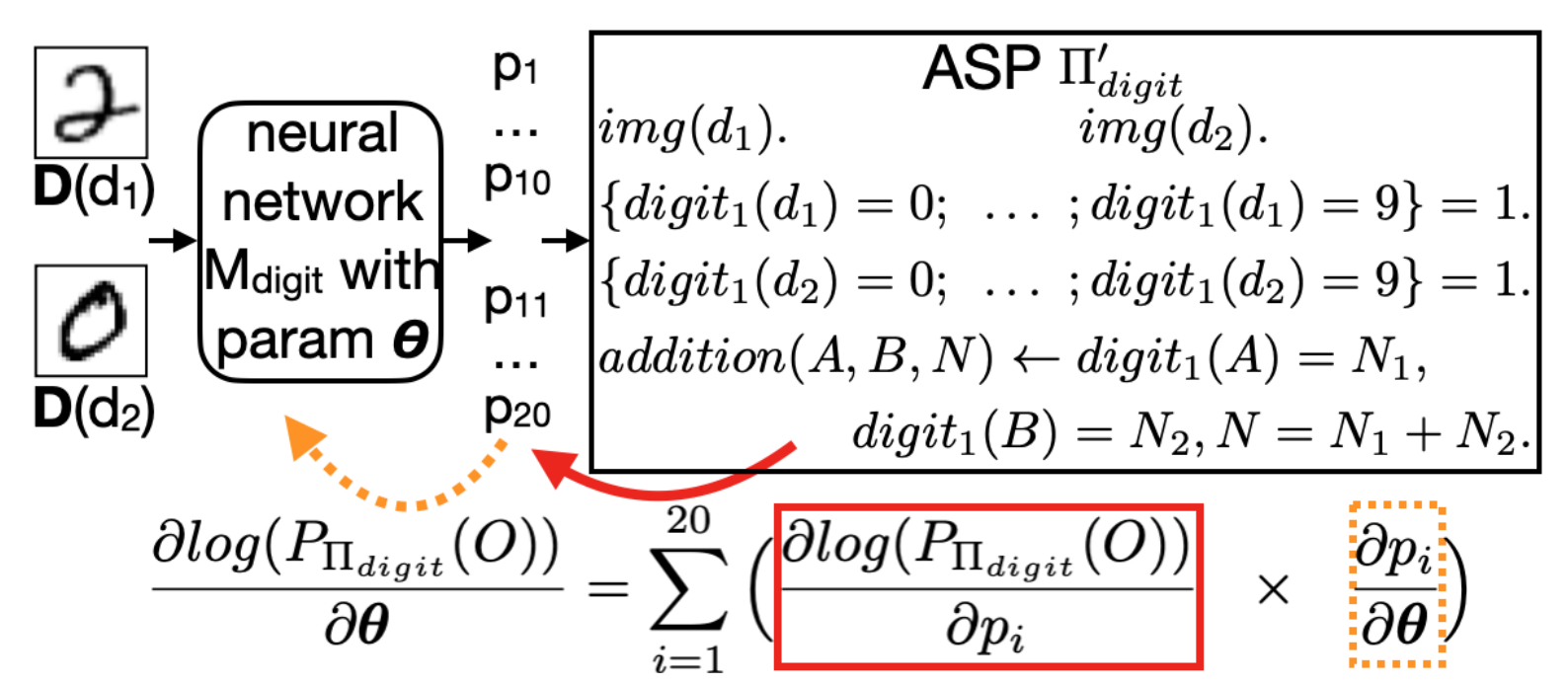
In the above figure the red arrow indicates the gradient calculateion of the ASP program w.r.t the neural network outputs. This is calculated by using a formula given by the authors in the paper. Since the program is not continuous the gradient is difficult to calculate. The orange arrow indicates the calculateion of gradients of the outputs of the neural network w.r.t the network parameters. This is simply done using backpropogation.
Inference
The inference procedure is straightforward wherein a trained neural network is used through the nn() atom in the ASP program to solve the problem.
Pros
- The impovement paper shows over DeepProblog
is notable. There is a significant improvement in terms of convergence time. - Seemless integration and a strong proposition for combining neural networks and ASP in the training loop.
- ASP is more expressive than prolog so it could be seen as a slight advantage over DeepProblog which uses prolog like semantics in terms of knowledge representation.
Cons
- No theoretical proof to show that the given proposition for gradient calculation is correct and is optimal. (Atleast for me it seems like there is some exposition into the insight behind this is needed here.)
- SCALABILITY is a big issue. It is simply not scalable for bigger and more complex problems since ASP is used. ASP solvers like CLINGO ground the whole program and then find the stable models which simply becomes intractable.
This framework falls under the Symbolic[Neuro] category of neurosymbolic systems according to the taxonomy given by Henry Kautz