Problog
A probabilistic extension of prolog
Introduction
Problog
Background
1) Monotone Disjunctive Normal Form (DNF): A DNF with no negated literals.
2) Binary Decision Diagrams (BDDs) : A BDD is an acyclic directed graph with two terminal nodes 0 and 1. Each non-terminal node is labeled with a variable. The edges are labeled with 0 or 1. The BDD represents a boolean function. The BDD is constructed by recursively splitting the variables into two sets and then recursively constructing the BDD for each set. The BDD is constructed by splitting the variables in such a way that the number of nodes in the BDD is minimized.
Example Program
1.0 :: likes(X,Y):- friendof(X,Y).
0.8 :: likes(X,Y):- friendof(X,Z), likes(Z,Y).
0.5 :: friendof(john,mary).
0.5 :: friendof(mary,pedro).
0.5 :: friendof(mary,tom).
0.5 :: friendof(pedro,tom).
Inference
In Problog the success probability $P(q|T)$ of the query $q$ in a ProbLog program $T$ is computed. Where \(T = \{ p_1 : c_1, ..., p_n: c_n \}\). The ProbLog program $T$ defines a probability distribution over all logic programs \(L \subseteq L_T = \{c_1, ..., c_n\}\) as follows:
\(\begin{align} P(L|T) &= \prod_{c_i \in L} p_i \prod_{c_i \notin L} (1-p_i) \label{eq_1} \end{align}\) Above is a formal way of stating that the probability of a logic program $L$ is the product of the probabilities of the clauses in $L$ and the complement of the clauses not in $L$.
The success probability of a query $q$ given a ProbLog program $T$ is defined as follows:
\[\begin{align} P(q|L) &= \begin{cases} 1 & \text{if } \exists \theta : L \vDash q\theta \\ 0 & \text{otherwise } \end{cases} \label{eq_2} \\ P(q,L|T) &= P(q|L)P(L|T) \label{eq_3} \\ P(q|T) &= \sum_{M \subseteq L_T} P(q,M|T) \label{eq_4} \end{align}\]As is apparent form eq. \(\eqref{eq_4}\) , the naive way of computing the probability is to enumerate all possible logic programs $M$ which is infeasible.
Hence, the authors propose first computing the proofs of $q$ in $L_T$ which results in a monotone DNF formula and then compute the probability of this formula.
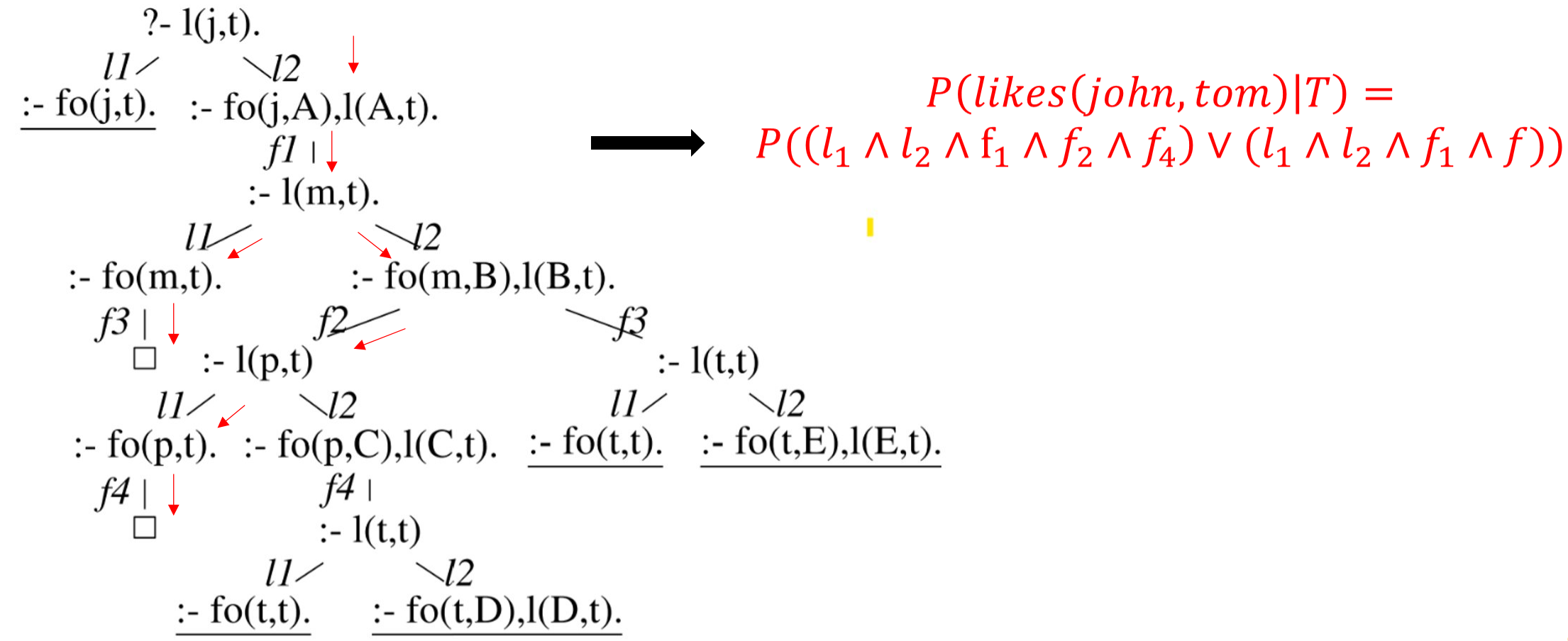
For a given query, $q$ the SLD-tree is fist constructed and a DNF is constructed from the tree where each clause in disjunction is a successful proof as shown in Figure 1.
Figure 1: SLD-tree to DNF
Now to calculate the $P((l_1 \land l_2 \land f_1 \land f_2 \land f_4) \lor (l_1 \land l_2 \land f_1 \land f_3))$ the authors construct a BDD which is a graphical representaion of a boolean function. Note, there are a lot of representations that can be used instead of a BDD. For instance SDD (Sentential Decision Diagrams). These were also used by Huang et. al in
An approximate inference algorithm was also proposed by the authors because the exact inference might not be feasible in all applications.
Conclusion
The major advantage of ProbLog over prolog is the functionality of adding probabilistic knowledge and hence working with uncertainity. Since the approximate inference algorithm is also proposed, one can find the probability of a query succeeding in a huge biological database wherein a possible connection between a certain gene and a disease can then be uncovered with a certain probability.
Questions that need to be addressed
Q) What is the SLD resolution?
SLD resolution is a proof procedure for Horn clauses. It is a generalization of the resolution principle for propositional logic. It is a top-down procedure. This is done by attempting to match the goal with the heads of the clauses in the database. When a match is found, the system attempts to satisfy the conditions in the body of the clause. If the body conditions can be satisfied, the goal is replaced with subgoals representing the body conditions. A tree of proofs thus generated is called the SLD tree.
Q) What category of problems does problog aim to solve that prolog cannot?
ProbLog is used in domains where there is uncertainity. The facts and rules that have been found for example are uncertain. They are only true with a certain probability. For example, in a biological database, the fact that a certain gene is responsible for a certain disease is uncertain.
Q) What are the strengths and weaknesses of the paper (problog)?
Strengths :
1) The inference is made more efficient because of the approximation algorithm of problog.
2) Most of the builtin predicates in prolog can be used directly.
Weakness :
1) It is very hard to scale to big databases because the SLD-tree has to be calculated and then the intermediate representation such as BDD, OBDD, SDD etc. has to be constructed for the DNF and then the probability has to be calculated. This is a very expensive process.
Q) Can there be a probscasp? I personally think there can definitely be a probscasp and that would be interesting to see. The problem is of course the scaling it up. A critical questions to be asked is would probscasp solve anything that problog cannot? Maybe the answer would come to me sometime soon. Until then I will keep thinking about it.